Die numerische Modellierung von Schallquellen hat in der Akustikforschung eine zentrale Bedeutung, und die Boundary Element Method (BEM) bietet hierbei ein kraftvolles Werkzeug zur präzisen Simulation akustischer Felder. Durch die effiziente Berechnung der Schallausbreitung an komplexen Strukturen ermöglicht BEM es, realitätsnahe Modelle zu erstellen, die sowohl in der Industrie als auch in der Forschung von unschätzbarem Wert sind. In diesem Artikel erfahren Sie, wie BEM die Herausforderungen der akustischen Modellierung meistert und welche Vorteile sie gegenüber anderen Methoden bietet. Lassen Sie uns die Details genauer betrachten.
Einleitung
Grundlagen
Schall
Definition
Schall ist ein physikalisches Phänomen, das durch die Ausbreitung von mechanischen Wellen in einem Medium entsteht, sei es in Luft, Wasser oder festen Stoffen. Diese Wellen entstehen durch die Störung des Gleichgewichtszustands der Moleküle in einem Medium, was zu Druckschwankungen führt, die sich in alle Richtungen ausbreiten. Das menschliche Ohr nimmt diese Druckschwankungen als Töne wahr, wobei die Frequenz der Wellen die Tonhöhe bestimmt und die Amplitude die Lautstärke beeinflusst. Schall ist somit eine wesentliche Komponente unserer Umwelt, die Kommunikation ermöglicht und Informationen über das Umfeld liefert.
Eigenschaften
Die Eigenschaften von Schall umfassen Frequenz, Wellenlänge, Amplitude und Geschwindigkeit. Die Frequenz, gemessen in Hertz (Hz), gibt die Anzahl der Schwingungen pro Sekunde an und bestimmt die Tonhöhe. Die Wellenlänge ist der Abstand zwischen zwei aufeinanderfolgenden Punkten gleicher Phase, wie etwa zwei aufeinanderfolgende Wellenberge, und steht in direkter Beziehung zur Frequenz. Die Amplitude beschreibt die Stärke der Schallwellen, was sich in der Lautstärke bemerkbar macht. Die Schallgeschwindigkeit variiert je nach Medium und ist in der Luft bei Raumtemperatur etwa 343 Meter pro Sekunde. Diese grundlegenden Eigenschaften sind entscheidend für das Verständnis der Schallausbreitung und deren Einfluss auf die Umwelt.
Modellierung
Ansätze
Die Modellierung von Schall ist ein entscheidender Bereich in der Akustik, der es ermöglicht, Schallquellen und deren Ausbreitung zu analysieren und zu simulieren. Es gibt verschiedene Ansätze, darunter analytische, numerische und experimentelle Methoden. Analytische Modelle verwenden mathematische Gleichungen, um Schallphänomene zu beschreiben, sind jedoch oft auf einfache Systeme beschränkt. Numerische Modelle, wie die Boundary Element Method (BEM), bieten die Möglichkeit, komplexe Geometrien und Randbedingungen zu berücksichtigen. Experimentelle Ansätze hingegen beinhalten physische Messungen zur Validierung von Modellen oder zur direkten Untersuchung von Schallquellen. Jeder dieser Ansätze hat seine eigenen Vor- und Nachteile und wird je nach Anwendungsfall gewählt.
Vorteile
Die numerische Modellierung von Schall bietet zahlreiche Vorteile, die sie zu einem unverzichtbaren Instrument in der modernen Akustik machen. Einer der Hauptvorteile ist die Fähigkeit, komplexe Geometrien und Randbedingungen in die Berechnungen einzubeziehen, was mit analytischen Methoden oft nicht möglich ist. Darüber hinaus ermöglicht sie die Untersuchung von Szenarien, die experimentell schwer realisierbar oder kostspielig wären. Die Flexibilität und Genauigkeit der numerischen Modelle machen sie zu einem bevorzugten Werkzeug für Ingenieure und Wissenschaftler, die sich mit der Planung und Analyse von akustischen Systemen beschäftigen. Die Boundary Element Method ist ein besonders effektiver Ansatz, da sie nur die Oberfläche eines Körpers diskretisiert, was die Rechenzeit und den Ressourcenbedarf reduziert.
Methoden
BEM
Grundprinzip
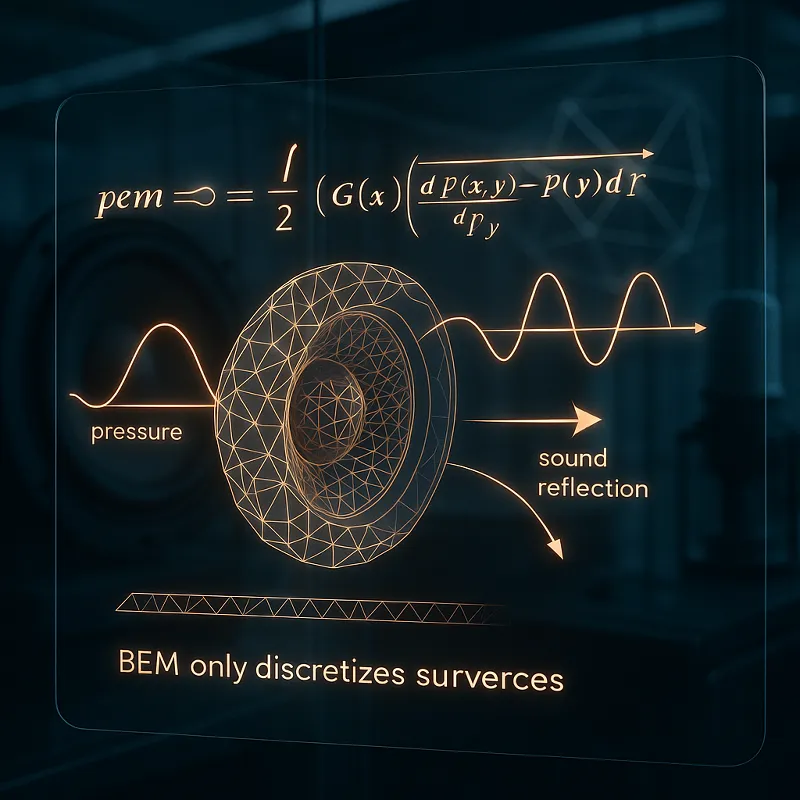
Die Boundary Element Method (BEM) ist eine numerische Technik zur Lösung von Randwertproblemen, die bei der Modellierung von Schallquellen und deren Ausbreitung eingesetzt wird. Im Gegensatz zu anderen Methoden, die das gesamte Volumen eines Mediums diskretisieren, konzentriert sich BEM auf die Randflächen. Dies reduziert den Rechenaufwand erheblich und ermöglicht die effiziente Berechnung von Schallfeldern in und um komplexe Strukturen. BEM basiert auf der Lösung von Integralgleichungen, die die Beziehung zwischen den Randwerten eines Problems und den Feldgrößen im Inneren des untersuchten Bereichs beschreiben. Diese Methode ist besonders nützlich in der Akustik, da sie die präzise Modellierung von Schallreflexion, -streuung und -absorption an Oberflächen ermöglicht.
Geschichte
Die Geschichte der Boundary Element Method reicht bis in die Mitte des 20. Jahrhunderts zurück, als sie erstmals in der Strömungsmechanik entwickelt wurde. Erst in den 1960er und 1970er Jahren fand sie in der Akustik Anwendung, als Forscher erkannten, dass die Methode besonders gut geeignet war, um die komplexen Wechselwirkungen zwischen Schallwellen und den Oberflächen zu modellieren, an denen sie reflektiert oder absorbiert werden. Die Weiterentwicklung von BEM wurde durch die zunehmende Rechenleistung von Computern und die Verbesserung numerischer Algorithmen vorangetrieben, was zu ihrer breiten Akzeptanz in der Wissenschaft und Industrie führte. Heute ist BEM ein Standardwerkzeug in der Akustik, das in zahlreichen Anwendungen von der Architekturakustik bis zur Fahrzeugentwicklung eingesetzt wird.
Nichtlineare akustische Wellen in dissipativen Medien 👆Schallquellen
Typen
Punktquellen
Eigenschaften
Punktquellen sind ideale Schallquellen, die Schallwellen gleichmäßig in alle Richtungen abgeben. Sie werden oft als theoretisches Modell verwendet, um die Ausbreitung von Schall in einem Medium zu verstehen. Eine der grundlegenden Eigenschaften von Punktquellen ist, dass ihre Schallintensität mit dem Quadrat der Entfernung abnimmt. Dies nennt man das quadratische Abstandsverhalten. Diese Eigenschaft erleichtert die mathematische Modellierung und Berechnung von Schallfeldern, da sie eine vereinfachte Annahme über die räumliche Verteilung des Schalls ermöglicht. In der Praxis gibt es jedoch kaum perfekte Punktquellen, da reale Schallquellen oft komplexere Strahlungsmuster aufweisen.
Anwendungen
Punktquellen finden in vielen Bereichen der Akustik Anwendung. In der Umweltakustik werden sie verwendet, um die Schallausbreitung von Verkehrslärm zu modellieren. In der Architekturakustik sind sie nützlich, um die Akustik von Räumen zu analysieren und die Verteilung von Schallenergie zu optimieren. Sie werden auch in der Lautsprechertechnik eingesetzt, um die Eigenschaften von Lautsprechersystemen zu testen und zu verbessern. Trotz ihrer theoretischen Natur sind sie ein unverzichtbares Werkzeug, um komplexe akustische Probleme zu lösen und fundierte Vorhersagen über die Schallausbreitung zu treffen.
Linienquellen
Eigenschaften
Linienquellen unterscheiden sich von Punktquellen dadurch, dass sie Schall entlang einer Linie abstrahlen. Diese Art von Schallquelle ist besonders in Situationen relevant, in denen Schall über längere Strecken und in bestimmten Richtungen verteilt werden muss. Ein markantes Merkmal von Linienquellen ist, dass ihre Schallintensität proportional zur Entfernung abnimmt, was sie besonders effizient für die Schallübertragung entlang von Korridoren oder in Röhren macht. Aufgrund ihrer geometrischen Eigenschaften sind Linienquellen auch in der Lage, Schallenergie gezielter zu lenken und zu kontrollieren. Dies macht sie zu einem wertvollen Werkzeug in der Schallfeldmodellierung.
Anwendungen
In der Praxis werden Linienquellen häufig in der Straßen- und Eisenbahnplanung verwendet, um die Auswirkung von Lärm auf die Umgebung zu bewerten. Sie sind auch in der Beschallungstechnik weit verbreitet, insbesondere in großen Veranstaltungsorten, wo es darauf ankommt, den Schall gleichmäßig über das Publikum zu verteilen. In der Umweltakustik helfen Linienquellen dabei, die Lärmbelastung durch kontinuierliche Schallquellen wie Verkehrsstraßen oder Eisenbahnlinien zu modellieren. Ihre Fähigkeit, Schall gezielt zu lenken, macht sie auch in der Architekturakustik zu einem wichtigen Element bei der Gestaltung von akustisch komplexen Räumen.
Modelle
Mathematisch
Formeln
Die mathematische Modellierung von Schallquellen ist ein essenzieller Bestandteil der Akustikwissenschaft. Für Punktquellen wird häufig die Gleichung I = P / (4πr²) verwendet, wobei I die Schallintensität, P die abgestrahlte Leistung und r die Entfernung zur Quelle darstellt. Diese Formel illustriert das quadratische Abstandsverhalten, das typisch für Punktquellen ist. Für Linienquellen wird die Formel I = P / (2πrL) angewandt, wobei L die Länge der Linie ist. Diese mathematischen Modelle sind grundlegend für die Berechnung und Vorhersage von Schallfeldern in verschiedenen Anwendungen.
Beispiele
Ein klassisches Beispiel für die Anwendung mathematischer Modelle von Punktquellen ist die Berechnung der Schallverteilung in einem Konzertsaal. Hierbei wird analysiert, wie sich der Schall von einer zentralen Bühne ausbreitet und welche Bereiche des Publikums am besten beschallt werden. Für Linienquellen findet man Anwendungen in der Berechnung der Lärmbelastung entlang von Eisenbahnstrecken. Hierbei wird untersucht, wie sich der Lärm in der Umgebung ausbreitet und welche Schutzmaßnahmen ergriffen werden müssen, um die Lärmbelastung in Wohngebieten zu reduzieren. Diese Beispiele verdeutlichen die Notwendigkeit präziser mathematischer Modelle in der Akustik.
Numerisch
Tools
In der modernen Akustik spielen numerische Werkzeuge eine entscheidende Rolle. Software wie COMSOL Multiphysics und ANSYS bietet umfassende Möglichkeiten zur Simulation und Analyse von Schallquellen. Diese Werkzeuge ermöglichen es, komplexe akustische Szenarien zu modellieren, die mit analytischen Methoden nur schwer zu erfassen wären. Sie bieten die Möglichkeit, detaillierte Schallfeldsimulationen durchzuführen und verschiedene Szenarien zu testen, ohne dass physische Experimente nötig sind. Dadurch können Ingenieure und Wissenschaftler fundierte Entscheidungen treffen und effizientere und umweltfreundlichere Akustiklösungen entwickeln.
Algorithmen
Algorithmen spielen eine zentrale Rolle in der numerischen Modellierung von Schallquellen. Die Finite-Elemente-Methode (FEM) und die Boundary-Elemente-Methode (BEM) sind zwei weit verbreitete Ansätze, die es ermöglichen, die akustische Umgebung detailliert zu simulieren. Diese Algorithmen verwenden komplexe mathematische Modelle, um die Interaktionen zwischen Schallwellen und ihrer Umgebung zu berechnen. Sie sind besonders nützlich bei der Analyse von Schallausbreitungsproblemen in komplexen geometrischen Strukturen. Durch die Verwendung dieser Algorithmen können Wissenschaftler genaue Vorhersagen über die Ausbreitung von Schall treffen und optimierte Designs für akustische Systeme entwickeln.
BEM Technik
Grundlagen
Theorie
Die Boundary Element Method (BEM) ist eine numerische Technik, die insbesondere in der Akustik zur Simulation von Schallquellen eingesetzt wird. Diese Methode basiert auf der Lösung von Randwertproblemen, bei denen nur die Oberfläche des untersuchten Bereichs diskretisiert wird. Im Gegensatz zu volumetrischen Methoden wie der Finite-Elemente-Methode (FEM), reduziert BEM die Dimension des Problems um eins, was zu einer erheblichen Verringerung des Rechenaufwands führen kann. BEM basiert auf den Grundprinzipien der mathematischen Physik und verwendet Integralgleichungen, um die Schallfeldverteilung zu berechnen. Diese Integralgleichungen resultieren aus der Anwendung der Green’schen Funktion, die als fundamentale Lösung der Helmholtz-Gleichung fungiert. Die Helmholtz-Gleichung beschreibt die Ausbreitung von Schallwellen in homogenen Medien, indem sie die Beziehung zwischen dem Schalldruck und der Frequenz der Schwingungen herstellt.
Mathematik
Die mathematischen Grundlagen von BEM stützen sich stark auf Integralgleichungen, die die Beziehung zwischen den Feldgrößen auf der Oberfläche und im Inneren des untersuchten Bereichs herstellen. Eine der zentralen Gleichungen ist die Helmholtz-Integralgleichung, die die akustischen Felder beschreibt. Diese Gleichung wird durch die Diskretisierung der Oberfläche in eine endliche Anzahl von Elementen gelöst, wobei jedes Element durch seine Knotenpunkte beschrieben wird. Die Lösung der Integralgleichung erfordert die Berechnung von Einflusskoeffizienten, die die Wirkung eines Elementes auf andere beschreiben. Diese Koeffizienten werden durch die numerische Integration der Green’schen Funktion bestimmt. Die Verwendung dieser mathematischen Modelle ermöglicht es, komplexe Schallquellen und deren Wechselwirkungen präzise zu simulieren.
Annahmen
Bei der Anwendung der BEM-Technik müssen bestimmte Annahmen getroffen werden, um die Modellierung zu vereinfachen. Eine grundlegende Annahme ist die Linearität des akustischen Mediums, was bedeutet, dass die Superposition von Wellenformen gültig ist. Diese Annahme ermöglicht es, die komplexen Interaktionen von Schallwellen zu analysieren, ohne die nichtlinearen Effekte berücksichtigen zu müssen. Eine weitere Annahme betrifft die Homogenität des Mediums, in dem sich die Schallwellen ausbreiten. Diese Annahme vereinfacht die mathematischen Berechnungen, indem sie konstante Materialeigenschaften im gesamten Untersuchungsbereich voraussetzt. Schließlich wird oft angenommen, dass die Schallwellen harmonisch sind, was die Lösung der Helmholtz-Gleichung erleichtert, da sie auf eine feste Frequenz beschränkt ist.
Implementierung
Schritte
Die Implementierung der Boundary Element Method umfasst mehrere wesentliche Schritte. Zunächst wird die Geometrie des Problems definiert, indem die Oberfläche des Untersuchungsbereichs in diskrete Elemente unterteilt wird. Dieser Prozess wird als Diskretisierung bezeichnet und erfordert präzise Meshing-Techniken, um eine genaue Darstellung der Oberfläche zu gewährleisten. Nach der Diskretisierung folgt die Formulierung der Integralgleichungen, die die Beziehung zwischen den akustischen Feldgrößen beschreiben. Diese Gleichungen werden anschließend in ein System linearer Gleichungen umgewandelt, das die unbekannten Feldgrößen auf den Elementknoten enthält. Die Lösung dieses Gleichungssystems erfordert effiziente numerische Verfahren, die eine schnelle und stabile Berechnung ermöglichen.
Software
Für die numerische Implementierung der BEM-Technik gibt es spezialisierte Softwarepakete, die den Anwendern eine benutzerfreundliche Umgebung zur Verfügung stellen. Diese Softwarelösungen bieten umfassende Werkzeuge für die Geometrieerstellung, Meshing, Formulierung der Integralgleichungen und Lösung der resultierenden Gleichungssysteme. Einige der bekanntesten BEM-Softwarepakete sind BEM++ und ANSYS, die eine breite Palette von Anwendungen in der Akustik und im Ingenieurwesen abdecken. Diese Programme nutzen fortschrittliche Algorithmen, um die Berechnungen zu optimieren und die Genauigkeit der Ergebnisse zu erhöhen. Durch die Verwendung dieser Software können Ingenieure und Forscher komplexe akustische Probleme effizient analysieren und lösen.
Anwendungen
Akustik
Simulation
In der Akustik wird die Boundary Element Method häufig zur Simulation von Schallquellen und ihrer Ausbreitung eingesetzt. Diese Methode ermöglicht es, die akustische Leistung von Lautsprechern, Mikrofonen und anderen audiotechnischen Geräten präzise zu simulieren. Durch die Analyse der Schallfeldverteilung können Ingenieure die Positionierung und Gestaltung von Schallquellen optimieren, um eine gleichmäßige Schallverteilung zu gewährleisten. Darüber hinaus ermöglicht die BEM-Technik die Untersuchung der Wechselwirkungen zwischen Schallquellen und der umgebenden Architektur, was für die Gestaltung von Konzertsälen und Auditorien von entscheidender Bedeutung ist.
Optimierung
Die BEM-Technik bietet auch wertvolle Werkzeuge zur Optimierung akustischer Systeme. Durch die Simulation verschiedener Designkonfigurationen können Ingenieure die besten Lösungen identifizieren, die den gewünschten akustischen Anforderungen entsprechen. Diese Optimierungsprozesse können die Form und das Material von Schallquellen sowie ihre Platzierung in einem Raum umfassen. Mit BEM können auch akustische Parameter wie Schalldruckpegel und Nachhallzeit optimiert werden, um eine optimale Klangqualität zu erreichen. Solche Optimierungen sind in der Automobilindustrie, im Bauwesen und in der Unterhaltungselektronik von großer Bedeutung, um Produkte zu entwickeln, die den höchsten akustischen Standards entsprechen.
Ingenieurwesen
Fallstudien
Im Ingenieurwesen haben sich zahlreiche Fallstudien mit der Anwendung der BEM-Technik befasst, um komplexe akustische Probleme zu lösen. Eine bemerkenswerte Fallstudie betrifft die Entwicklung von geräuscharmen Flugzeugtriebwerken, bei denen BEM zur Analyse der Schallausbreitung und zur Reduzierung der Lärmemissionen eingesetzt wurde. Weitere Fallstudien umfassen die Untersuchung von Lärmschutzwänden entlang von Autobahnen, bei denen die Effektivität verschiedener Designs bewertet wurde, um den Verkehrslärm zu minimieren. Diese Studien veranschaulichen die Vielseitigkeit der BEM-Technik und ihre Fähigkeit, in verschiedenen ingenieurtechnischen Anwendungen wertvolle Einblicke zu bieten.
Ergebnisse
Die Ergebnisse der BEM-Anwendungen im Ingenieurwesen zeigen deutliche Verbesserungen in der akustischen Leistung und Lärmminderung. In der Luftfahrtindustrie haben Optimierungen auf Basis von BEM zu leiseren Flugzeugtriebwerken geführt, die den internationalen Lärmschutzstandards entsprechen. Im Bauwesen hat BEM dazu beigetragen, effektive Lärmschutzlösungen zu entwickeln, die den Komfort in Wohn- und Arbeitsumgebungen erhöhen. Diese Ergebnisse unterstreichen die Bedeutung der BEM-Technik als unverzichtbares Werkzeug in der modernen Akustikforschung und Ingenieurpraxis.
Forschung
Trends
Innovationen
Die numerische Modellierung von Schallquellen mittels der Boundary Element Method (BEM) hat in den letzten Jahren erhebliche Fortschritte gemacht. Diese Technik ermöglicht es, Schallprobleme mit hoher Präzision zu simulieren und zu analysieren. Ein entscheidender Trend ist die Verbesserung der Rechenleistung und der Algorithmen, die es ermöglichen, komplexere Modelle in kürzerer Zeit zu berechnen. Forschungseinrichtungen weltweit arbeiten daran, die Effizienz und Genauigkeit dieser Methoden weiter zu steigern. Dies geschieht unter anderem durch die Integration von Künstlicher Intelligenz (KI) und maschinellem Lernen, die helfen, Vorhersagen zu verbessern und die Anpassbarkeit der Modelle zu erhöhen.
Technologien
Die technologischen Entwicklungen in der BEM-Forschung sind bemerkenswert. High-Performance-Computing-Systeme (HPC) und Cloud-Computing ermöglichen die Bearbeitung von großen Datenmengen und komplexen Simulationen, die vorher undenkbar waren. Diese Technologien bieten nicht nur mehr Rechenleistung, sondern auch eine bessere Zugänglichkeit für Forscher, die über begrenzte Ressourcen verfügen. Parallel dazu werden neue Softwarelösungen entwickelt, die die Benutzerfreundlichkeit erhöhen und den Zugang zu fortschrittlichen Modellierungstools erleichtern.
Entwicklungen
Innerhalb der BEM-Forschung gibt es kontinuierliche Entwicklungen in der Modellierung von Materialeigenschaften und geometrischen Besonderheiten. Die Fähigkeit, Materialien mit anisotropen (richtungsabhängigen) Eigenschaften zu modellieren, öffnet neue Möglichkeiten in der Simulation von realistischen Szenarien, wie sie in der Automobil- oder Luftfahrtindustrie vorkommen. Diese Entwicklungen tragen dazu bei, die Vorhersagen von Schallausbreitungen zu präzisieren und so die Lärmminderung und Akustikoptimierung in verschiedenen Anwendungen zu verbessern.
Herausforderungen
Probleme
Obwohl die Fortschritte erheblich sind, steht die Forschung zur numerischen Modellierung von Schallquellen mit BEM vor mehreren Herausforderungen. Eine der größten Hürden ist die Skalierbarkeit der Modelle. Komplexe Modelle erfordern immense Rechenressourcen, was sowohl in Bezug auf Kosten als auch auf Energieverbrauch problematisch sein kann. Außerdem kann die Genauigkeit der Modellergebnisse durch Unsicherheiten in den Eingangsdaten oder durch numerische Instabilitäten beeinträchtigt werden. Diese Probleme erfordern kontinuierliche Forschung und Optimierung.
Lösungen
Zur Bewältigung dieser Herausforderungen werden verschiedene Lösungen erforscht. Eine vielversprechende Strategie ist die Entwicklung von adaptiven Algorithmen, die die Recheneffizienz verbessern, indem sie nur die relevanten Bereiche eines Modells mit hoher Genauigkeit simulieren. Des Weiteren wird an der Verbesserung der Datenqualität gearbeitet, indem fortschrittliche Messmethoden für die Eingabedaten entwickelt werden. Diese Maßnahmen sollen die Zuverlässigkeit und Effizienz der Modellierungen erhöhen und somit die Anwendung der BEM in der Praxis erleichtern.
Zukunft
Prognosen
Erwartungen
Die Zukunft der numerischen Modellierung von Schallquellen mittels BEM sieht vielversprechend aus. Experten erwarten, dass die Technologie in den nächsten Jahren noch weiter an Bedeutung gewinnen wird, insbesondere in Branchen wie der Automobil- und Luftfahrtindustrie, wo akustische Optimierungen entscheidend sind. Die Weiterentwicklung von KI und maschinellem Lernen wird voraussichtlich die Anpassungsfähigkeit und Präzision der Modelle weiter verbessern, was zu noch effizienteren Lösungen führt.
Möglichkeiten
Neue Möglichkeiten eröffnen sich durch die Integration von BEM in interdisziplinäre Forschungsprojekte. Durch die Kombination mit anderen Modellierungstechniken, wie der Finite-Elemente-Methode (FEM), können umfassendere und genauere Simulationen erstellt werden. Dies könnte die Tür zu völlig neuen Anwendungen öffnen, wie etwa der Entwicklung von intelligenten akustischen Materialien oder der Optimierung von Lärmschutzmaßnahmen in urbanen Umgebungen.
Visionen
Konzept
Die Visionen für die Zukunft der BEM-Technologie umfassen die Schaffung von vollintegrierten Systemen, die nahtlos in bestehende technische Infrastrukturen eingebunden werden können. Ziel ist es, eine benutzerfreundliche Plattform zu entwickeln, die es Anwendern ermöglicht, akustische Modelle ohne tiefgehende technische Kenntnisse zu erstellen und zu analysieren. Dies könnte die Akzeptanz und Anwendung der Technologie in verschiedenen Bereichen erheblich steigern.
Umsetzung
Die Umsetzung dieser Vision erfordert eine enge Zusammenarbeit zwischen Forschern, Ingenieuren und Industriepartnern. Es ist entscheidend, dass die entwickelten Lösungen nicht nur theoretisch fundiert, sondern auch praktisch anwendbar sind. Durch Pilotprojekte und Kooperationen sollen die entwickelten Technologien getestet und optimiert werden, um sicherzustellen, dass sie den Anforderungen der Praxis gerecht werden. Die Beteiligung der Industrie ist dabei besonders wichtig, um sicherzustellen, dass die entwickelten Lösungen marktgerecht und wirtschaftlich tragfähig sind.
FAQ
Was ist die Boundary Element Method (BEM)?
Die Boundary Element Method (BEM) ist eine numerische Technik zur Lösung von Randwertproblemen, die insbesondere in der Akustik und Elektrodynamik Anwendung findet. Sie konzentriert sich auf die Modellierung der Oberflächen eines Objekts, anstatt das gesamte Volumen zu simulieren.
Wie verbessert BEM die Schallmodellierung?
BEM verbessert die Schallmodellierung, indem es eine genaue Simulation der Schallausbreitung ermöglicht, insbesondere in komplexen Geometrien. Durch die Konzentration auf die Ränder reduziert es den Rechenaufwand im Vergleich zu volumetrischen Methoden.
Welche Rolle spielt KI in der BEM-Forschung?
Künstliche Intelligenz (KI) spielt eine zunehmende Rolle in der BEM-Forschung, indem sie hilft, Vorhersagen zu verbessern und Modelle zu optimieren. KI kann Muster erkennen und lernen, effizientere Algorithmen zu entwickeln.
Welche Industrien profitieren von BEM?
Industrien wie die Automobil- und Luftfahrtbranche profitieren erheblich von BEM. Die Methode hilft, den Lärmpegel zu reduzieren und die Akustik von Fahrzeugen und Flugzeugen zu optimieren, was zu besseren Produkten führt.
Was sind die Hauptvorteile der BEM-Technologie?
Die Hauptvorteile der BEM-Technologie sind ihre Effizienz und Genauigkeit bei der Modellierung von Schallproblemen, insbesondere in komplexen geometrischen Umgebungen. Sie ermöglicht genaue Simulationen mit weniger Rechenaufwand im Vergleich zu anderen Methoden.